Brief History of Filter Design

The advent of electronic filtering occurred in the beginning of the 20th century. In 1915, to be precise. Karl Willy Wagner from Germany, and George Campbell from the United States discovered that a ladder network consisting of inductors and capacitors could separate signals of different frequencies. This is what a filter of this kind looks like.

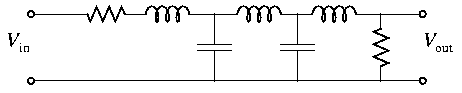
This is a simple example: a lowpass filter. Different architectures can realize bandpass, highpass, allpass, bandstop, or multiple-band pass filters. Every combination of pass- and stopbands is possible, but the transitory area's between the pass- and stopbands behave badly and are badly defined.

One of the first people to solve this problem was S. Butterworth, who made filters out of simple and overseeable sections, separated by valve amplifiers, and published it in 1930. One of his filter sections looks like this.

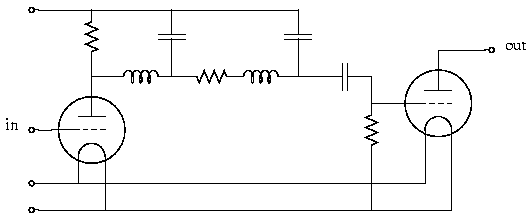
This is one of the first active filters. It has a well defined transient between the passband and stopband, and nowadays we call the response he created the "maximally flat" or "Butterworth" response. Actually, around the same time, William Bennett made filters with the same response, and he managed to do this with passive components only. Other people who did important work to make the transfer characteristic of filters designable were Sidney Darlington and Wilhelm Cauer.

The filters of that time were all built with capacitors and inductors. Capacitors were generally of a higher quality than inductors. Therefore, people started looking for methods to realize filters with capacitors and without inductors. R.P. Sallen and E.L. Key found a way to do this with active elements. This is one of their proposed filter sections, published in 1955.

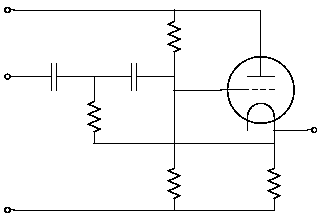
This is what most active filters still are today. Capacitors, no inductors, and amplification.

Active Filters

Sallen and Key filters are still in use today. The filters nowadays contain operational amplifiers in stead of valves. Especially in discrete applications they are attractive, because only one active element is necessary to build a filter of a theoretically arbitrary order. And the voltage gain of the active element does not need to be high. Sometimes unity gain is sufficient.

For integrated filters, this setup is less practical. Resistors and capacitors with an accurate value are usually not realizable on a chip. For that reason, tuning is necessary. Especially tuning of the resistor values is popular. This requires the use of tunable resistors, which are non-linear. A Sallen-and-Key filter does not handle these non-linearities gracefully. The filters that are in use in integrated form usually have a number of active elements (opamps or transconductors) that is equal to the order of the filter at least. After all, active elements, which used to be the most expensive elements in the valve era, are the cheapest elements in the chip age.

Quadrivium's Home Page